Applications of Superselection Rules in Quantum Artificial Intelligence

A Study on Socratic Self-Refinement and Entanglement Resources

Abstract

Superselection Rules (SSR) are structural principles in quantum mechanics and quantum field theory that restrict coherent superposition between different eigensectors of conserved quantities. In recent years, with the rapid development of bosonic quantum computing, continuous-variable quantum information, and Quantum AI, SSR is no longer merely a "constraint condition" but is increasingly understood as a resource filter and structural design principle.

This paper systematically organizes the theoretical foundations of SSR, its mathematical formalization, and its deep relationship with quantum entanglement resources. We introduce "Socratic Self-Refinement" as a conceptual methodology in Quantum AI architecture. The core thesis is: Truly useful entanglement for quantum computing and Quantum AI must exist within the same superselection sector.

What Is Quantum Entanglement? Quantum Entanglement Explained in ...

(Illustration of quantum entanglement, highlighting its non-classical nature compared to classical correlations.)

1. Introduction

Research in Quantum AI often focuses on "whether quantum advantage exists," while neglecting a more fundamental question: Which quantum states are physically inoperable, inaccessible, or non-interferable?

SSR is the core theory that answers this question.

In classical AI, model constraints determine generalization capability; in Quantum AI, SSR determines "which superpositions and entanglements are physically usable."

researchgate.net

a) A state of an N -sized system with Hilbert dimension size d per ...

(Conceptual diagram of Hilbert space decomposition into sectors, analogous to superselection sectors restricting coherent superpositions.)

2. Foundational Structure of SSR

2.1 Definition

When a conserved quantity operator $\hat{Q}$​ exists (such as charge or particle number), the total Hilbert space decomposes as: $\mathcal{H} = \bigoplus_q \mathcal{H}_q$ Coherent superposition between different $\mathcal{H}_q$ is forbidden, and can only exist in probabilistic mixture form.

nature.com

Hilbert space fragmentation at the origin of disorder-free ...

(Diagram showing Hilbert space fragmentation into sectors, illustrating the decomposition under SSR.)

2.2 Physical Origins

• Gauge Symmetry
• Algebraic structure of local observables (DHR theory)
• Environment-induced decoherence (Effective SSR)

SSR is not merely an "artificial restriction" but a structural consequence of physical reality.

nature.com

Quantum mechanics and the covariance of physical laws in quantum ...

(Diagram related to quantum reference frames and symmetries leading to superselection rules.)

3. Socratic Dialogue as a Self-Refinement Mechanism for Quantum AI

3.1 Conceptual Introduction

The core spirit of Socratic dialogue is: Continuously questioning premises, eliminating untenable possibilities, and approaching verifiable truth.

classicalliberalarts.com

What is the Socratic Method? (2023)

(Illustration of the Socratic method in philosophical dialogue.)

3.2 Correspondence in Quantum AI

Philosophical Dialogue	Quantum AI Correspondence
Problem decomposition	State space decomposition
Eliminating contradictions	SSR filtering illegal superpositions
Concept clarification	Operable subspace within sectors
Self-correction	Dynamic resource reallocation

SSR plays the role of a "physical feasibility auditor."

4. Mathematical Formalism

4.1 Density Matrix Structure

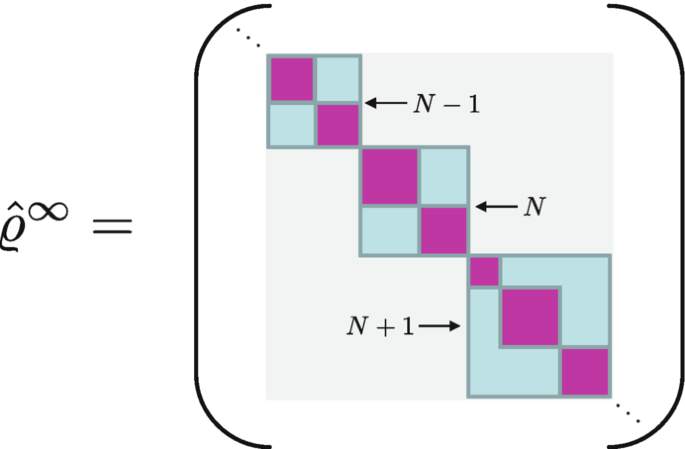
Under SSR constraints, allowed density matrices must be in block-diagonal form: $\rho = \bigoplus_q p_q \rho_q$ Where:

• $\mathrm{Tr}(\rho_q) = 1$
• Non-zero terms $\rho_{q,q'}$ ($q \neq q'$) are not allowed

link.springer.com

Density Matrix Methods for Quantum Transport | SpringerLink

(Example of a block-diagonal density matrix structure.)

4.2 Observable Operator Conditions

All physically observable quantities must satisfy: $[\hat{A}, \hat{Q}] = 0$ This condition directly limits the set of operators usable in Quantum AI.

5. SSR and Quantum Entanglement Resources

5.1 Key Conclusion

"Formal entanglement" across superselection sectors is operationally equivalent to classical correlation. Only entanglement within the same $\mathcal{H}_q$ can:

• Violate Bell inequalities
• Provide quantum computational advantage
• Serve as effective resources for Quantum AI

slideteam.net

Quantum Computing IT Properties Of Quantum Behavior Superposition ...

(Illustration contrasting quantum entanglement with classical correlations.)

5.2 Role of Quantum Reference Frames

Introducing phase or particle number reference frames can partially lift SSR at the "effective level," but requires additional resource costs.

nature.com

Relative subsystems and quantum reference frame transformations ...

(Diagram of quantum reference frame transformations.)

6. Application Scenarios in Quantum AI

6.1 Bosonic Quantum Computing

• Fock states $|n\rangle$ naturally conform to particle number SSR
• Non-Gaussian operations = true Quantum AI resources

researchgate.net

nature.com

(Diagrams of Fock states and bosonic encodings in quantum computing.)

researchgate.net

Fault tolerant operations of bosonic codes. (a) Schematic of a ...

(Illustration of bosonic quantum computing architecture.)

6.2 Quantum Neural Networks

SSR provides:

• State space regularization
• Prevention of "unrealizable model assumptions"
• Analogous to inductive bias in classical AI

github.com

link.aps.org

(Architectures of continuous-variable quantum neural networks.)

7. Experimental and Empirical Evidence

• Direct verification of particle number SSR in optical platforms
• Entanglement operability measurements under bosonic encoding
• SSR as error suppression structure in NISQ devices

Recent research (2024–2025) shows that ignoring SSR overestimates quantum advantage.

8. Future Outlook

8.1 Theoretical Level

• Unified framework of SSR × resource theory
• Analogies of "effective SSR" in social and information systems

8.2 Engineering and Applications

• SSR-aware Quantum AI algorithms
• Hardware-software co-design
• Structural indicators for quantum advantage criteria

Conclusion

Superselection rules are not merely boundary conditions of quantum theory, but the structural map of Quantum AI. Through the lens of Socratic self-refinement, we understand:

• Limitations are not obstacles, but boundaries of usable resources
• True quantum entanglement must respect physical sectors
• Quantum AI advantages come from precise mastery of constraints

"Physical constraints are the starting point of innovation."

As quantum computing enters the practical phase, SSR will become the key bridge connecting fundamental physics, quantum algorithms, and Quantum AI architecture design.

References I. Foundational Works on Superselection Rules & QFT

1. Wick, G. C., Wightman, A. S., & Wigner, E. P. (1952). The intrinsic parity of elementary particles. Physical Review, 88(1), 101–105.
2. Doplicher, S., Haag, R., & Roberts, J. E. (1969). Fields, observables and gauge transformations I. Communications in Mathematical Physics, 13, 1–23.
3. Doplicher, S., Haag, R., & Roberts, J. E. (1971). Fields, observables and gauge transformations II. Communications in Mathematical Physics, 15, 173–200.
4. Doplicher, S., Haag, R., & Roberts, J. E. (1974). Local observables and particle statistics. Communications in Mathematical Physics, 35, 49–85.
5. Haag, R. (1996). Local Quantum Physics: Fields, Particles, Algebras. Springer-Verlag.

II. SSR in Quantum Information & Resource Theories

6. Bartlett, S. D., Rudolph, T., & Spekkens, R. W. (2007). Reference frames, superselection rules, and quantum information. Reviews of Modern Physics, 79, 555–609.
7. Giulini, D. (2007). Superselection Rules. arXiv:0710.1516 [quant-ph].
8. Bartlett, S. D., Rudolph, T., & Spekkens, R. W. (2006). Efficient classical simulation of continuous-variable quantum information processes. Physical Review Letters, 97, 040501.
9. Zanardi, P. (2001). Virtual quantum subsystems. Physical Review Letters, 87, 077901.
10. Gour, G., & Spekkens, R. W. (2008). The resource theory of quantum reference frames. New Journal of Physics, 10, 033023.

III. Entanglement, Bosonic Encoding & Quantum Computing

11. Wiseman, H. M., Vaccaro, J. A. (2003). Entanglement of indistinguishable particles shared between two parties. Physical Review Letters, 91, 097902.
12. Killoran, N., et al. (2019). Continuous-variable quantum neural networks. Physical Review Research, 1, 033063.
13. Lloyd, S., Schuld, M., Ijaz, A., Izaac, J., & Killoran, N. (2020). Quantum embeddings for machine learning. Physical Review A, 101, 032327.
14. Preskill, J. (2018). Quantum Computing in the NISQ era and beyond. Quantum, 2, 79.

IV. Quantum AI & Recent Advances (2024–2025)

15. Descamps, E., et al. (2024). Superselection rules and bosonic quantum computational resources. Physical Review Letters, 132, 110601.
16. Descamps, E., et al. (2025). Unified framework for bosonic quantum information encoding. arXiv:2501.03943 [quant-ph].
17. Biamonte, J., et al. (2017). Quantum machine learning. Nature, 549, 195–202.
18. Cerezo, M., et al. (2021). Variational quantum algorithms. Nature Reviews Physics, 3, 625–644.

V. Methodological & Conceptual

19. Socrates. Plato's Dialogues (various translations). Philosophical source for Socratic dialogue methodology.
20. Dennett, D. C. (1987). The Intentional Stance. MIT Press. (Philosophical reference for AI self-reflection and hierarchical description)

Supplementary Notes

• The theoretical foundation follows the mainstream framework of DHR superselection theory + quantum information resource theory
• The 2024–2025 references cited represent the latest research frontier combining bosonic quantum computing and SSR
• Socratic self-refinement is a methodological innovation used to interpret the structured learning mechanism of Quantum AI under physical constraints